Arrheniusgraph

Als Arrheniusgraphen (auch Arrheniusdarstellung oder Arrheniusplot) wird eine spezielle graphische Darstellung der Temperaturabhängigkeit einer Größe (z. B. die Geschwindigkeitskonstante einer chemischen Reaktion) bezeichnet, in der der Logarithmus der Größe über dem Kehrwert der Temperatur aufgetragen wird. Dadurch werden Zusammenhänge, die mit einer Arrhenius-Gleichung beschreibbar sind, als eine Gerade dargestellt. Verwendet wird diese Art der Auftragung bei verschiedenen chemischen oder physikalischen Vorgängen.

Anwendung

Formelsymbole
E A {\displaystyle E_{\mathrm {A} }} Aktivierungsenergie J mol−1
k B {\displaystyle k_{\mathrm {B} }} Boltzmann-Konstante 1.381e-23 J K−1
R {\displaystyle R} universelle Gaskonstante 8,314 J mol−1 K−1
N A {\displaystyle N_{\mathrm {A} }} Avogadro-Konstante 6.022e23 mol−1
T {\displaystyle T} absolute Temperatur K

Gilt für eine Größe k {\displaystyle k} in ihrer Abhängigkeit von der Temperatur T {\displaystyle T} der Zusammenhang

k = k 0 ⋅ e − E A k B ⋅ T {\displaystyle k=k_{0}\cdot \mathrm {e} ^{-{\frac {E_{\mathrm {A} }}{k_{\mathrm {B} }\cdot T}}}\qquad } (für einzelne Teilchen mit der Boltzmann-Konstanten)

oder

k = k 0 ⋅ e − E A R ⋅ T {\displaystyle k=k_{0}\cdot \mathrm {e} ^{-{\frac {E_{\mathrm {A} }}{R\cdot T}}}\qquad } (makroskopisch mit der universellen Gaskonstanten)

oder für deren Zahlenwert { k } {\displaystyle \{k\}}

{ k } = { k 0 } e − E A R ⋅ T {\displaystyle \{k\}=\{k_{0}\}\,\mathrm {e} ^{-{\frac {E_{\mathrm {A} }}{R\cdot T}}}}

und wird dieses logarithmiert zu

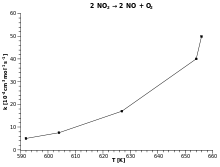
ln ⁡ { k } = ln ⁡ { k 0 } − E A R ⋅ 1 T {\displaystyle \ln\{k\}=\ln\{k_{0}\}-{\frac {E_{\mathrm {A} }}{R}}\cdot {\frac {1}{T}}}  ,
Zerfall Stickstoffdioxid
2 NO2 → 2 NO + O2
Geschwindigkeitskonstante über der Temperatur mit linear geteilten Achsen
Arrheniusgraph

dann ergibt sich diese Gleichung mit y = ln ⁡ { k } {\displaystyle y=\ln\{k\}} und x = 1 T {\displaystyle x={\frac {1}{T}}} als Geradengleichung

y = b + m ⋅ x {\displaystyle y=b+m\cdot x}

mit der Steigung m = − E A R {\displaystyle m=-{\frac {E_{\mathrm {A} }}{R}}} .

Werden aus Messungen gewonnene Werte von ln ⁡ { k } {\displaystyle \ln\{k\}} als y {\displaystyle y} über 1 T {\displaystyle {\frac {1}{T}}} als x {\displaystyle x} in einem kartesischen Koordinatensystem auf linear geteilten Achsen aufgetragen, so sollte sich eine Gerade ergeben. Aus ihrer Steigung m = Δ y Δ x {\displaystyle m={\tfrac {\Delta y}{\Delta x}}} lässt sich die Aktivierungsenergie E A {\displaystyle E_{\mathrm {A} }} ausrechnen.

Gleichwertige Aussagen ergeben sich mit dem dekadischen Logarithmus mit

y = lg ⁡ { k } {\displaystyle y=\lg\{k\}} , x = 1 T {\displaystyle x={\frac {1}{T}}} und m = − E A R lg ⁡ e = − E A 2,302 6 R {\displaystyle m=-{\frac {E_{\mathrm {A} }}{R}}\,\lg \mathrm {e} =-{\frac {E_{\mathrm {A} }}{2{,}3026\;R}}} .

Beispiele

Naturgesetze, die im Arrheniusgraph linear dargestellt werden, sind beispielsweise die Temperaturabhängigkeit

  • der Reaktionsgeschwindigkeit einer Reaktion erster Ordnung,
  • des Diffusionskoeffizienten in festen Stoffen sowie
  • der Eigenleitungsdichte in Halbleitern.

Wenn aufgrund von theoretischen Betrachtungen eine entsprechende Gesetzmäßigkeit vermutet wird, kann diese Annahme mit Hilfe der Arrheniusdarstellung beurteilt werden. Wird der Arrheniusgraph nicht geradlinig, so ist offenbar der untersuchte Zusammenhang nicht durch die Arrhenius-Gleichung beschreibbar (in der Kinetik: keine Reaktionen erster Ordnung).

In nebenstehendem Beispiel wird die Annahme einer Reaktion erster Ordnung bestätigt; die Steigung kann abgelesen und berechnet werden und daraus die Aktivierungsenergie.

Quellen