Kac-Moody-Algebra

Kac-Moody-Algebren, benannt nach Victor Kac und Robert Moody, sind in der mathematischen Theorie der Lie-Algebren untersuchte Algebren. Man geht von einer Matrix mit bestimmten Eigenschaften aus und wendet darauf ein Verfahren an, das an die klassische Konstruktion einer endlichdimensionalen halbeinfachen Lie-Algebra aus einer vorgegebenen Cartan-Matrix angelehnt ist. Man kann dann drei Typen solcher Kac-Moody-Algebren ausmachen. Die Algebren vom endlichen Typ (s. u.) sind die aus der klassischen Theorie bekannten endlichdimensionalen halbeinfachen Lie-Algebren, so dass die Theorie der Kac-Moody-Algebren als eine Verallgemeinerung der klassischen Theorie angesehen werden kann. Dazu kommen zwei weitere Typen, der affine Typ und der indefinite Typ (s. u.), die weder endlichdimensional noch halbeinfach sind.

Eine ${\displaystyle n\times n}$-Matrix ${\displaystyle A=(A_{i,j})}$ heißt verallgemeinerte Cartan-Matrix, falls

• Alle Koeffizienten sind ganzzahlig, das heißt ${\displaystyle A_{i,j}\in \mathbb {Z} }$ für alle ${\displaystyle i,j=1,\ldots ,n}$
• ${\displaystyle A_{i,i}=2}$ für alle ${\displaystyle i=1,\ldots ,n}$
• ${\displaystyle A_{i,j}\leq 0}$ für alle ${\displaystyle i,j=1,\ldots ,n,\,i\not =j}$
• Aus ${\displaystyle A_{i,j}=0}$ folgt stets ${\displaystyle A_{j,i}=0}$ für alle ${\displaystyle i,j=1,\ldots ,n}$.

Offenbar sind Cartan-Matrizen Beispiele für verallgemeinerte Cartan-Matrizen.

Zwei verallgemeinerte ${\displaystyle n\times n}$-Cartan-Matrizen ${\displaystyle A=(A_{i,j})}$ und ${\displaystyle A'=(A'_{i,j})}$ heißen äquivalent, wenn es eine Permutation ${\displaystyle \sigma }$ auf ${\displaystyle \{1,\ldots ,n\}}$ gibt mit ${\displaystyle A'_{i,j}=A_{\sigma (i),\sigma (j)}}$ gibt.

Eine verallgemeinerte Cartan-Matrix heißt zerlegbar, wenn sie zu einer Matrix der Form

${\displaystyle {\begin{pmatrix}A_{1}&0\\0&A_{2}\end{pmatrix}}}$

mit Untermatrizen ${\displaystyle A_{1}}$ und ${\displaystyle A_{2}}$ äquivalent ist, sonst unzerlegbar.

Zu einer vorgegebenen verallgemeinerten ${\displaystyle n\times n}$-Cartan-Matrix ${\displaystyle A=(A_{i,j})}$ gibt es

• einen endlichdimensionalen ${\displaystyle \mathbb {C} }$-Vektorraum ${\displaystyle H}$
• eine linear unabhängige Teilmenge ${\displaystyle \Pi ^{\vee }=\{h_{1},\ldots ,h_{n}\}\subset H}$,
• eine linear unabhängige Teilmenge ${\displaystyle \Pi =\{\alpha _{1},\ldots ,\alpha _{n}\}\subset H^{*}}$, wobei ${\displaystyle H^{*}}$ der Dualraum von ${\displaystyle H}$ ist,

so dass ${\displaystyle A_{i,j}=\alpha _{j}(h_{i})}$ für alle ${\displaystyle i,j=1,\ldots ,n}$

Die Daten ${\displaystyle (H,\Pi ^{\vee },\Pi )}$ nennt man eine Realisierung von ${\displaystyle A}$. Man kann zeigen, dass die Dimension von ${\displaystyle H}$ mindestens ${\displaystyle 2n-\mathrm {rang} (A)}$ ist, wobei ${\displaystyle \mathrm {rang} (A)}$ der Rang der Matrix ist, dass dieses Minimum angenommen wird, und dass es zu je zwei Realisierungen ${\displaystyle (H_{1},\Pi _{1}^{\vee },\Pi _{1})}$ und ${\displaystyle (H_{2},\Pi _{2}^{\vee },\Pi _{2})}$ minimaler Dimension einen Vektorraumisomorphismus ${\displaystyle \varphi :H_{1}\rightarrow H_{2}}$ gibt, der ${\displaystyle \Pi _{1}^{\vee }}$ auf ${\displaystyle \Pi _{2}^{\vee }}$ abbildet und dessen duale Abbildung ${\displaystyle \Pi _{2}}$ auf ${\displaystyle \Pi _{1}}$ abbildet. Diese sogenannten minimalen Realisierungen sind also bis auf Isomorphie eindeutig bestimmt.^[1]

Bislang haben wir zu einer verallgemeinerten ${\displaystyle n\times n}$-Cartan-Matrix ${\displaystyle A=(A_{i,j})}$ eine minimale Realisierung ${\displaystyle (H,\Pi ^{\vee }=\{h_{1},\ldots ,h_{n}\},\Pi =\{\alpha _{1},\ldots ,\alpha _{n}\})}$ konstruiert. Diese Daten verwenden wir nun, um eine Lie-Algebra ${\displaystyle {\tilde {L}}(A)}$ aus Erzeugern und Relationen zu definieren. Die Menge der Erzeuger ist

${\displaystyle X=\{e_{1},\ldots ,e_{n},f_{1},\ldots ,f_{n}\}\cup \{{\tilde {x}}\mid x\in H\}}$.

Die Elemente sind nur Symbole, lediglich die Matrizengröße ${\displaystyle n}$ und der Vektorraum ${\displaystyle H}$ gehen hier ein. Die Relationen sind

• ${\displaystyle {\tilde {x}}-\lambda {\tilde {y}}-\mu {\tilde {z}}}$   für alle ${\displaystyle x,y,z\in H,\,\lambda ,\mu \in \mathbb {C} }$   mit ${\displaystyle x=\lambda x+\mu z}$
• ${\displaystyle [{\tilde {x}}{\tilde {y}}]}$   für alle   ${\displaystyle x,y\in H}$
• ${\displaystyle [e_{i}f_{i}]-{\tilde {h_{i}}}}$   für alle   ${\displaystyle i=1,\ldots ,n}$
• ${\displaystyle [e_{i}f_{j}]}$   für alle   ${\displaystyle i,j=1,\ldots ,n,\,i\not =j}$
• ${\displaystyle [{\tilde {x}}e_{i}]-\alpha _{i}(x)}$   für alle   ${\displaystyle i=1,\ldots ,n,\,x\in H}$
• ${\displaystyle [{\tilde {x}}f_{i}]+\alpha _{i}(x)}$   für alle   ${\displaystyle i=1,\ldots ,n,\,x\in H}$

Bezeichnet ${\displaystyle R}$ die Menge dieser Relationen, so setzen wir

${\displaystyle {\tilde {L}}(A):=L(X;R)}$, wobei letztere die durch die Erzeuger ${\displaystyle X}$ und Relationen ${\displaystyle R}$ definierte Lie-Algebra sei.

Die ersten beiden Gruppen von Relationen führen offensichtlich dazu, dass ${\displaystyle H\mapsto {\tilde {H}}:=\{{\tilde {x}}\mid x\in H\},\,x\mapsto {\tilde {x}}}$ ein Lie-Algebren-Homomorphismus zwischen abelschen Lie-Algebren ist. Man kann sogar zeigen, dass dieser ein Isomorphismus ist.

Zu einer verallgemeinerten Cartan-Matrix ${\displaystyle A=(A_{i,j})}$ haben wir eine Lie-Algebra ${\displaystyle {\tilde {L}}(A)}$ mit einer darin enthaltenen abelschen Unteralgebra ${\displaystyle {\tilde {H}}}$ konstruiert. Man kann nun zeigen, dass

${\displaystyle I:=\sum \{J\mid \,J\subset {\tilde {L}}(A){\text{ Lie-Ideal mit }}J\cap {\tilde {H}}=\{0\}\}}$

wieder ein Ideal mit ${\displaystyle I\cap {\tilde {H}}=\{0\}}$ ist. Man nennt

${\displaystyle L(A):={\tilde {L}}(A)/I}$

die Kac-Moody-Algebra zur verallgemeinerten Cartan-Matrix ${\displaystyle A}$.

Man kann zeigen, dass die Isomorphieklasse von ${\displaystyle L(A)}$ nur von der Äquivalenzklasse der verallgemeinerten Cartan-Matrix abhängt, insbesondere nicht von der Wahl einer minimalen Realisierung. Ist ${\displaystyle A}$ sogar eine Cartan-Matrix, so ist die Kac-Moody-Algebra zu ${\displaystyle A}$ isomorph zur endlichdimensionalen halbeinfachen Lie-Algebra mit dieser Cartan-Matrix.^[2]

Die Kac-Moody-Algebren zu unzerlegbaren verallgemeinerten Cartan-Matrizen zerfallen in drei Typen. Sie werden durch Eigenschaften der zugrunde liegenden verallgemeinerten Cartan-Matrix definiert. Dazu beachte, dass solche Matrizen ganzzahlige und damit reellwertige Koeffizienten haben und daher auf dem ${\displaystyle \mathbb {R} ^{n}}$, dem Vektorraum der Spaltenvektoren, operieren. Auf dem ${\displaystyle \mathbb {R} ^{n}}$ sei die komponentenweise Ordnung ${\displaystyle \leq }$ gegeben, das heißt ${\displaystyle u\leq v}$, falls komponentenweise ${\displaystyle u_{i}\leq v_{i}}$ gilt. Wir schreiben entsprechend ${\displaystyle u<v}$, falls komponentenweise ${\displaystyle u_{i}<v_{i}}$ gilt.

Man verwendet die folgenden Typbezeichnungen, für die ${\displaystyle A}$ eine unzerlegbare verallgemeinerte ${\displaystyle n\times n}$-Cartan-Matrix sei, sowohl für ${\displaystyle A}$ als auch für die Kac-Moody-Algebra ${\displaystyle L(A)}$.^[3]

${\displaystyle A}$ und damit auch ${\displaystyle L(A)}$ hat endlichen Typ, falls

• ${\displaystyle \det(A)\not =0}$,
• Es gibt ${\displaystyle u\in \mathbb {R} ^{n}}$ mit ${\displaystyle u>0}$ und ${\displaystyle Au>0}$,
• Aus ${\displaystyle Au\geq 0}$ folgt ${\displaystyle u>0}$ oder ${\displaystyle u=0}$.

${\displaystyle A}$ und damit auch ${\displaystyle L(A)}$ hat affinen Typ, falls

• ${\displaystyle \mathrm {rang} (A)=n-1}$, das heißt der Korang ist 1,
• Es gibt ${\displaystyle u\in \mathbb {R} ^{n}}$ mit ${\displaystyle u>0}$ und ${\displaystyle Au=0}$,
• Aus ${\displaystyle Au\geq 0}$ folgt ${\displaystyle Au=0}$.

${\displaystyle A}$ und damit auch ${\displaystyle L(A)}$ hat indefiniten Typ, falls

• Es gibt ${\displaystyle u\in \mathbb {R} ^{n}}$ mit ${\displaystyle u>0}$ und ${\displaystyle Au<0}$,
• Aus ${\displaystyle Au\geq 0}$ und ${\displaystyle u\geq 0}$ folgt ${\displaystyle u=0}$.

Es ist nicht offensichtlich, dass dies tatsächlich eine Dreiteilung der unzerlegbaren verallgemeinerten Cartan-Matrizen darstellt. Alternativ kann man diese drei Typen für unzerlegbare verallgemeinerte Cartan-Matrizen wie folgt charakterisieren:

• ${\displaystyle A}$ hat endlichen Typ genau dann, wenn es ${\displaystyle u\in \mathbb {R} ^{n}}$ gibt mit ${\displaystyle u>0}$ und ${\displaystyle Au>0}$
• ${\displaystyle A}$ hat affinen Typ genau dann, wenn es ${\displaystyle u\in \mathbb {R} ^{n}}$ gibt mit ${\displaystyle u>0}$ und ${\displaystyle Au=0}$
• ${\displaystyle A}$ hat indefiniten Typ genau dann, wenn es ${\displaystyle u\in \mathbb {R} ^{n}}$ gibt mit ${\displaystyle u>0}$ und ${\displaystyle Au<0}$

Man kann zeigen, dass Kac-Moody-Algebren endlichen Typs genau die endlichdimensionalen einfachen Lie-Algebren sind. Die Kac-Moody-Algebren affinen oder indefiniten Typs sind weder halbeinfach, sie haben ein nicht-triviales Zentrum, noch endlichdimensional.

Man kann, ganz ähnlich wie in der Theorie der endlich-dimensionalen halbeinfachen Lie-Algebren, jeder verallgemeinerten Cartan-Matrix ein Dynkin-Diagramm zuordnen, dies geschieht nach folgenden Regeln: Das Dynkin-Diagramm zur verallgemeinerten ${\displaystyle n\times n}$-Cartan-Matrix ${\displaystyle A=(A_{i,j})}$ ist ein Graph aus ${\displaystyle n}$ Knoten, die mit ${\displaystyle 1,\ldots ,n}$ bezeichnet werden. Für die Kanten zwischen diesen Knoten verfährt man wie folgt:

• Ist ${\displaystyle A_{i,j}A_{j,i}=0}$, so werden die Knoten ${\displaystyle i}$ und ${\displaystyle j}$ nicht verbunden.
• Ist ${\displaystyle A_{i,j}A_{j,i}=1}$, so werden die Knoten ${\displaystyle i}$ und ${\displaystyle j}$ durch eine einzelne Kante verbunden.
• Ist ${\displaystyle A_{i,j}A_{j,i}=2}$, so werden die Knoten ${\displaystyle i}$ und ${\displaystyle j}$ durch zwei Kanten verbunden. Ein >-Zeichen durch diese Kanten zeigt mit der Spitze auf ${\displaystyle i}$, wenn ${\displaystyle A_{i,j}=-2}$, sonst nach ${\displaystyle j}$.
• Ist ${\displaystyle A_{i,j}A_{j,i}=3}$, so werden die Knoten ${\displaystyle i}$ und ${\displaystyle j}$ durch drei Kanten verbunden. Ein >-Zeichen durch diese Kanten zeigt mit der Spitze auf ${\displaystyle i}$, wenn ${\displaystyle A_{i,j}=-3}$, sonst nach ${\displaystyle j}$.
• Ist ${\displaystyle A_{i,j}A_{j,i}=4}$ und ${\displaystyle |A_{i,j}|\not =|A_{j,i}|}$, so werden die Knoten ${\displaystyle i}$ und ${\displaystyle j}$ durch vier Kanten verbunden. Ein >-Zeichen durch diese Kanten zeigt mit der Spitze auf ${\displaystyle i}$, wenn ${\displaystyle A_{i,j}=-4}$, sonst nach ${\displaystyle j}$.
• Ist ${\displaystyle A_{i,j}A_{j,i}=4}$ und ${\displaystyle A_{i,j}=A_{j,i}=-2}$, so werden die Knoten ${\displaystyle i}$ und ${\displaystyle j}$ durch zwei Kanten verbunden. Ein >- und ein <-Zeichen werden durch diese Kanten gezeichnet, sie zeigen mit ihren Spitzen aufeinander.
• Ist ${\displaystyle A_{i,j}A_{j,i}\geq 5}$, so werden die Knoten ${\displaystyle i}$ und ${\displaystyle j}$ durch eine einzelne Kante verbunden und die ganzen Zahlen ${\displaystyle |A_{i,j}|}$ und ${\displaystyle |A_{j,i}|}$ wird an dieser Kante vermerkt.

Es ist klar, dass man aus dem Dynkin-Diagramm die verallgemeinerte Cartan-Matrix zurückgewinnen kann, ebenso, dass eine verallgemeinerte Cartan-Matrix genau dann unzerlegbar ist, wenn ihr Dynkin-Diagramm zusammenhängend ist.

In der klassischen Theorie, das heißt für unzerlegbare verallgemeinerte Cartan-Matrizen endlichen Typs, erhält man die bekannte Liste der Dynkin-Diagramme ${\displaystyle A_{n},B_{n},C_{n},D_{n},E_{6},E_{7},E_{8},F_{4},G_{2}}$, die eine vollständige Klassifikation der endlichdimensionalen einfachen Lie-Algebren darstellt. Für unzerlegbare verallgemeinerte Cartan-Matrizen affinen Typs gelingt ebenfalls eine vollständige Klassifikation, auch hier erhält man eine überschaubare Liste. Die zuletzt genannte Regel zur Erstellung des Dynkin-Diagramms findet im affinen Fall keine Anwendung, das kommt erst bei unzerlegbaren verallgemeinerten Cartan-Matrizen indefiniten Typs vor.^[4]

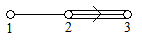
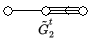
Als Beispiel für eine verallgemeinerte Cartan-Matrix affinen Typs betrachten wir

${\displaystyle {\tilde {G}}_{2}={\begin{pmatrix}2&-1&0\\-1&2&-1\\0&-3&2\end{pmatrix}}}$.

Die Bezeichnung ${\displaystyle {\tilde {G}}_{2}}$ stammt von einer Klassifikation der unzerlegbaren Cartan-Matrizen affinen Typs. Da

${\displaystyle {\begin{pmatrix}2&-1&0\\-1&2&-1\\0&-3&2\end{pmatrix}}\cdot {\begin{pmatrix}1\\2\\3\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}}$,

liegt nach oben genannten Kriterien tatsächlich ein affiner Typ vor: Es gibt ein ${\displaystyle u>0}$ mit ${\displaystyle {\tilde {G}}_{2}u=0}$. Das zugehörige Dynkin-Diagramm wird in nebenstehender Zeichnung wiedergegeben.

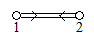
Ein weiteres Beispiel für eine verallgemeinerte Cartan-Matrix affinen Typs ist

${\displaystyle {\tilde {A}}_{1}={\begin{pmatrix}2&-2\\-2&2\end{pmatrix}}}$.

Zur Erstellung des Dynkin-Diagramms findet die vorletzte Regel Anwendung.

Hier ist die vollständige Liste aller Dynkin-Diagramme zu unzerlegbaren, verallgemeinerten Cartan-Matrizen affinen Typs:

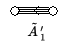
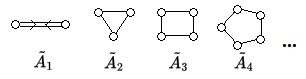
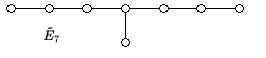
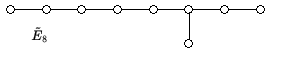
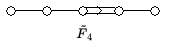
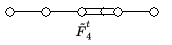
Die angegebenen Bezeichnungen der Dynkin-Diagramme sind Standardbezeichnungen. Die verwendete Tilde weist auf eine gewisse Affinisierung hin, das heißt auf einen Prozess, mit dem man aus gegebenen Lie-Algebren weitere erzeugen kann. Die zu diesen Dynkin-Diagrammen gehörigen Kac-Moody-Algebren werden genauso bezeichnet, das heißt man spricht von Kac-Moody-Algebren ${\displaystyle {\tilde {A}}_{1}'}$, ${\displaystyle {\tilde {A}}_{n}}$, ${\displaystyle {\tilde {B}}_{n}}$, ${\displaystyle {\tilde {B}}_{n}^{t}}$, ${\displaystyle {\tilde {C}}_{n}}$, ${\displaystyle {\tilde {C}}_{n}^{t}}$, ${\displaystyle {\tilde {C}}_{n}'}$, ${\displaystyle {\tilde {D}}_{n}}$, ${\displaystyle {\tilde {E}}_{6}}$, ${\displaystyle {\tilde {E}}_{7}}$, ${\displaystyle {\tilde {E}}_{8}}$, ${\displaystyle {\tilde {F}}_{4}}$, ${\displaystyle {\tilde {F}}_{4}^{t}}$, ${\displaystyle {\tilde {G}}_{2}}$, ${\displaystyle {\tilde {G}}_{2}^{t}}$.

Für Kac-Moody-Algebren kann man weite Teile der auf Wurzelsystemen beruhenden Theorie endlichdimensionaler halbeinfacher Lie-Algebren analog aufstellen. Als Ersatz für die Cartan-Unteralgebra dient das Bild von ${\displaystyle {\tilde {H}}}$ in der Quotientenalgebra ${\displaystyle L(A)}$. Man kann zeigen, dass die Abbildung ${\displaystyle H\rightarrow L(A),\,x\mapsto {\tilde {x}}+I}$ injektiv ist. Man kann also ${\displaystyle H}$ als Unteralgebra von ${\displaystyle L(A)}$ auffassen. Damit ist eine Darstellung der Form

${\displaystyle L(A):=H\oplus \sum _{\alpha \in Q}L_{\alpha }}$     mit

${\displaystyle L_{\alpha }:=\{y\in L(A)\mid \,[xy]=\alpha (x)y{\text{ für alle }}x\in H\}}$

möglich, wobei die ${\displaystyle \alpha \in Q\subset H^{*}}$ wie üblich Gewichte heißen und sich ganzzahlig aus den ${\displaystyle \alpha _{1},\ldots ,\alpha _{n}\in \Pi \subset H^{*}}$ linear kombinieren lassen. Die Grundlagen dieser Theorie sind im mehrfach zitierten Lehrbuch von Roger Carter ausgearbeitet.

1. ↑ Roger Carter: Lie Algebras of Finite and Affine Type, Cambridge studies in advanced mathematics 96 (2005), ISBN 978-0-521-85138-1, Kapitel 14.1: Realisations of a square matrix
2. ↑ Roger Carter: Lie Algebras of Finite and Affine Type, Cambridge studies in advanced mathematics 96 (2005), ISBN 978-0-521-85138-1, Kapitel 14.3: The Kac-Moody algebra L(A)
3. ↑ Roger Carter: Lie Algebras of Finite and Affine Type, Cambridge studies in advanced mathematics 96 (2005), ISBN 978-0-521-85138-1, Kapitel 15.1: A trichotomy for indecomposable GCMs
4. ↑ Roger Carter: Lie Algebras of Finite and Affine Type, Cambridge studies in advanced mathematics 96 (2005), ISBN 978-0-521-85138-1, Kapitel 15.1: The classification of affine generalized Cartan matrices