Special case of the Euler-Lagrange equations
Part of a series of articles about Calculus ∫ a b f ′ ( t ) d t = f ( b ) − f ( a ) {\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)} Rolle's theorem Mean value theorem Inverse function theorem Differential
Definitions Concepts Differentiation notation Second derivative Implicit differentiation Logarithmic differentiation Related rates Taylor's theorem Rules and identities
Definitions Integration by
The Beltrami identity , named after Eugenio Beltrami , is a special case of the Euler–Lagrange equation in the calculus of variations .
The Euler–Lagrange equation serves to extremize action functionals of the form
I [ u ] = ∫ a b L [ x , u ( x ) , u ′ ( x ) ] d x , {\displaystyle I[u]=\int _{a}^{b}L[x,u(x),u'(x)]\,dx\,,} where a {\displaystyle a} b {\displaystyle b} u ′ ( x ) = d u d x {\displaystyle u'(x)={\frac {du}{dx}}} [1]
If ∂ L ∂ x = 0 {\displaystyle {\frac {\partial L}{\partial x}}=0}
L − u ′ ∂ L ∂ u ′ = C , {\displaystyle L-u'{\frac {\partial L}{\partial u'}}=C\,,}
where C [2] [note 1]
Derivation By the chain rule , the derivative of L
d L d x = ∂ L ∂ x d x d x + ∂ L ∂ u d u d x + ∂ L ∂ u ′ d u ′ d x . {\displaystyle {\frac {dL}{dx}}={\frac {\partial L}{\partial x}}{\frac {dx}{dx}}+{\frac {\partial L}{\partial u}}{\frac {du}{dx}}+{\frac {\partial L}{\partial u'}}{\frac {du'}{dx}}\,.} Because ∂ L ∂ x = 0 {\displaystyle {\frac {\partial L}{\partial x}}=0}
d L d x = ∂ L ∂ u u ′ + ∂ L ∂ u ′ u ″ . {\displaystyle {\frac {dL}{dx}}={\frac {\partial L}{\partial u}}u'+{\frac {\partial L}{\partial u'}}u''\,.} We have an expression for ∂ L ∂ u {\displaystyle {\frac {\partial L}{\partial u}}}
∂ L ∂ u = d d x ∂ L ∂ u ′ {\displaystyle {\frac {\partial L}{\partial u}}={\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,} that we can substitute in the above expression for d L d x {\displaystyle {\frac {dL}{dx}}}
d L d x = u ′ d d x ∂ L ∂ u ′ + u ″ ∂ L ∂ u ′ . {\displaystyle {\frac {dL}{dx}}=u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}+u''{\frac {\partial L}{\partial u'}}\,.} By the product rule , the right side is equivalent to
d L d x = d d x ( u ′ ∂ L ∂ u ′ ) . {\displaystyle {\frac {dL}{dx}}={\frac {d}{dx}}\left(u'{\frac {\partial L}{\partial u'}}\right)\,.} By integrating both sides and putting both terms on one side, we get the Beltrami identity,
L − u ′ ∂ L ∂ u ′ = C . {\displaystyle L-u'{\frac {\partial L}{\partial u'}}=C\,.} Applications Solution to the brachistochrone problem The solution to the brachistochrone problem is the cycloid. An example of an application of the Beltrami identity is the brachistochrone problem , which involves finding the curve y = y ( x ) {\displaystyle y=y(x)}
I [ y ] = ∫ 0 a 1 + y ′ 2 y d x . {\displaystyle I[y]=\int _{0}^{a}{\sqrt {{1+y'^{\,2}} \over y}}dx\,.} The integrand
L ( y , y ′ ) = 1 + y ′ 2 y {\displaystyle L(y,y')={\sqrt {{1+y'^{\,2}} \over y}}} does not depend explicitly on the variable of integration x {\displaystyle x}
L − y ′ ∂ L ∂ y ′ = C . {\displaystyle L-y'{\frac {\partial L}{\partial y'}}=C\,.} Substituting for L {\displaystyle L}
y ( 1 + y ′ 2 ) = 1 / C 2 (constant) , {\displaystyle y(1+y'^{\,2})=1/C^{2}~~{\text{(constant)}}\,,} which can be solved with the result put in the form of parametric equations
x = A ( ϕ − sin ϕ ) {\displaystyle x=A(\phi -\sin \phi )} y = A ( 1 − cos ϕ ) {\displaystyle y=A(1-\cos \phi )} with A {\displaystyle A} 1 2 C 2 {\displaystyle {\frac {1}{2C^{2}}}} ϕ {\displaystyle \phi } cycloid .[3]
Solution to the catenary problem A chain hanging from points forms a catenary . Consider a string with uniform density μ {\displaystyle \mu } l {\displaystyle l} D {\displaystyle D} arc length ,
l = ∫ S d S = ∫ s 1 s 2 1 + y ′ 2 d x , {\displaystyle l=\int _{S}dS=\int _{s_{1}}^{s_{2}}{\sqrt {1+y'^{2}}}dx,} where
S {\displaystyle S} is the path of the string, and
s 1 {\displaystyle s_{1}} and
s 2 {\displaystyle s_{2}} are the boundary conditions.
The curve has to minimize its potential energy
U = ∫ S g μ y ⋅ d S = ∫ s 1 s 2 g μ y 1 + y ′ 2 d x , {\displaystyle U=\int _{S}g\mu y\cdot dS=\int _{s_{1}}^{s_{2}}g\mu y{\sqrt {1+y'^{2}}}dx,} and is subject to the constraint
∫ s 1 s 2 1 + y ′ 2 d x = l , {\displaystyle \int _{s_{1}}^{s_{2}}{\sqrt {1+y'^{2}}}dx=l,} where
g {\displaystyle g} is the force of gravity.
Because the independent variable x {\displaystyle x} separable first order differential equation
L − y ′ ∂ L ∂ y ′ = μ g y 1 + y ′ 2 + λ 1 + y ′ 2 − [ μ g y y ′ 2 1 + y ′ 2 + λ y ′ 2 1 + y ′ 2 ] = C , {\displaystyle L-y\prime {\frac {\partial L}{\partial y\prime }}=\mu gy{\sqrt {1+y\prime ^{2}}}+\lambda {\sqrt {1+y\prime ^{2}}}-\left[\mu gy{\frac {y\prime ^{2}}{\sqrt {1+y\prime ^{2}}}}+\lambda {\frac {y\prime ^{2}}{\sqrt {1+y\prime ^{2}}}}\right]=C,} where
λ {\displaystyle \lambda } is the
Lagrange multiplier .
It is possible to simplify the differential equation as such:
g ρ y − λ 1 + y ′ 2 = C . {\displaystyle {\frac {g\rho y-\lambda }{\sqrt {1+y'^{2}}}}=C.} Solving this equation gives the hyperbolic cosine , where C 0 {\displaystyle C_{0}}
y = C μ g cosh [ μ g C ( x + C 0 ) ] − λ μ g . {\displaystyle y={\frac {C}{\mu g}}\cosh \left[{\frac {\mu g}{C}}(x+C_{0})\right]-{\frac {\lambda }{\mu g}}.} The three unknowns C {\displaystyle C} C 0 {\displaystyle C_{0}} λ {\displaystyle \lambda } l {\displaystyle l}
Notes References ^ Courant R , Hilbert D (1953). Methods of Mathematical Physics . Vol. I (First English ed.). New York: Interscience Publishers, Inc. p. 184. ISBN 978-0471504474 .^ Weisstein, Eric W. "Euler-Lagrange Differential Equation." From MathWorld--A Wolfram Web Resource. See Eq. (5). ^ This solution of the Brachistochrone problem corresponds to the one in — Mathews, Jon; Walker, RL (1965). Mathematical Methods of Physics . New York: W. A. Benjamin, Inc. pp. 307–9. 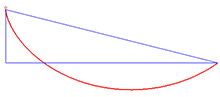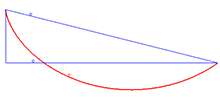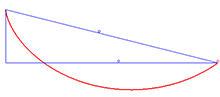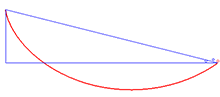


![{\displaystyle I[u]=\int _{a}^{b}L[x,u(x),u'(x)]\,dx\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90e683a73b0dc65988f0967cf70d6f3a9d6be522)














![{\displaystyle I[y]=\int _{0}^{a}{\sqrt {{1+y'^{\,2}} \over y}}dx\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6033bb9e89143c834ff902dd4ba14acae9eee035)




















![{\displaystyle L-y\prime {\frac {\partial L}{\partial y\prime }}=\mu gy{\sqrt {1+y\prime ^{2}}}+\lambda {\sqrt {1+y\prime ^{2}}}-\left[\mu gy{\frac {y\prime ^{2}}{\sqrt {1+y\prime ^{2}}}}+\lambda {\frac {y\prime ^{2}}{\sqrt {1+y\prime ^{2}}}}\right]=C,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa36083a7009e7eb0a1252456ece8c78a1f59ef8)



![{\displaystyle y={\frac {C}{\mu g}}\cosh \left[{\frac {\mu g}{C}}(x+C_{0})\right]-{\frac {\lambda }{\mu g}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30987f30cf86f34b3cdfbe8b4f09d33a45f1dcfe)











