Incentro

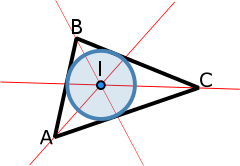
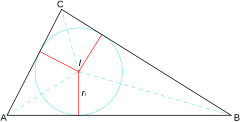
El Incentro de un triángulo (marcado con la letra I en el gráfico) es el punto en el que se cortan las tres bisectrices de sus ángulos internos. Equidista de los tres lados, y por lo tanto, es el centro de la circunferencia inscrita en el triángulo, tangente a sus tres lados.

Junto con el centroide (o baricentro) , circuncentro y ortocentro, es uno de los cuatro puntos notables del triángulo conocidos por los antiguos griegos, y el único que no se sitúa sobre la recta de Euler.

En la Enciclopedia de los Centros del Triángulo^[1]​ (obra del matemático estadounidense Clark Kimberling) es designado X(1) como la primera entrada de la lista de centros. Es el elemento identidad del grupo multiplicativo de los centros del triángulo.^[2]​^[3]​

Para polígonos con más de tres lados, el incentro solo existe en polígonos tangenciales -es decir, aquellos que tienen una circunferencia inscrita que es tangente a todos los lados del polígono. En este caso, el incentro es el centro de esta circunferencia y es equidistante de todos los lados.

Coordenadas cartesianas

Se pueden deducir las coordenadas cartesianas del incentro a partir de las coordenadas de los tres vértices del triángulo A, B y C. Si los vértices tienen por coordenadas ${\displaystyle (x_{a},y_{a})\,}$, ${\displaystyle (x_{b},y_{b})\,}$, y ${\displaystyle (x_{c},y_{c})\,}$, y los respectivos lados opuestos tienen longitudes ${\displaystyle a\,}$, ${\displaystyle b\,}$, y ${\displaystyle c\,}$, el incentro tendrá por coordenadas ${\displaystyle (x_{I},y_{I})\,}$:

${\displaystyle (x_{I},y_{I})={\frac {a(x_{a},y_{a})+b(x_{b},y_{b})+c(x_{c},y_{c})}{a+b+c}}={\bigg (}{\frac {ax_{a}+bx_{b}+cx_{c}}{a+b+c}},{\frac {ay_{a}+by_{b}+cy_{c}}{a+b+c}}{\bigg )}}$

Demostración

En efecto, Por el teorema de la bisectriz, aplicado a las bisectrices de los ángulos ${\displaystyle {\widehat {A}}}$ y ${\displaystyle {\widehat {B}}}$, se tiene que ${\displaystyle {\dfrac {c}{b}}={\dfrac {BP}{PC}}={\dfrac {BP}{BC-BP}}={\dfrac {BP}{a-BP}},}$ ${\displaystyle {\dfrac {c}{a}}={\dfrac {AQ}{QC}}={\dfrac {AQ}{AC-AQ}}={\dfrac {AQ}{b-AQ}}}$ resultando ${\displaystyle BP={\dfrac {ac}{b+c}},\qquad AQ={\dfrac {bc}{a+c}}}$ Sean los vectores ${\displaystyle {\overrightarrow {BP}}}$ y ${\displaystyle {\overrightarrow {AQ}}}$ Entonces: ${\displaystyle {\overrightarrow {BP}}={\dfrac {BP}{BC}}\,{\overrightarrow {BC}}={\dfrac {BP}{a}}\,{\overrightarrow {BC}}={\dfrac {c}{b+c}}\,{\overrightarrow {BC}},\qquad {\overrightarrow {AQ}}={\dfrac {AQ}{AC}}\,{\overrightarrow {AC}}={\dfrac {AQ}{b}}\,{\overrightarrow {AC}}={\dfrac {c}{a+c}}\,{\overrightarrow {AC}}}$ Para los vectores ${\displaystyle {\overrightarrow {AI}}}$ y ${\displaystyle {\overrightarrow {BI}}}$ existen los números reales ${\displaystyle \lambda }$ y ${\displaystyle \mu }$ con ${\displaystyle {\overrightarrow {AI}}=\lambda {\overrightarrow {AP}}}$ y ${\displaystyle {\overrightarrow {BI}}=\mu {\overrightarrow {BQ}}}$. Entonces, expresando el vector ${\displaystyle {\overrightarrow {AI}}}$ de estas dos formas, ${\displaystyle {\overrightarrow {AI}}=\lambda {\overrightarrow {AP}}}$ y ${\displaystyle {\overrightarrow {AI}}={\overrightarrow {AB}}+{\overrightarrow {BI}}}$, se tiene que: ${\displaystyle \left\{{\begin{array}{lcl}{\overrightarrow {AI}}&=&\lambda {\overrightarrow {AP}}=\lambda \left({\overrightarrow {AB}}+{\overrightarrow {BP}}\right)=\lambda \left({\overrightarrow {AB}}+{\dfrac {c}{b+c}}\,{\overrightarrow {BC}}\right)=\lambda {\overrightarrow {AB}}+{\dfrac {\lambda c}{b+c}}\,{\overrightarrow {BC}}\\{\overrightarrow {AI}}&=&{\overrightarrow {AB}}+{\overrightarrow {BI}}={\overrightarrow {AB}}+\mu {\overrightarrow {BQ}}={\overrightarrow {AB}}+\mu \left({\overrightarrow {BA}}+{\overrightarrow {AQ}}\right)={\overrightarrow {AB}}+\mu \left({\overrightarrow {BA}}+{\dfrac {c}{a+c}}\,{\overrightarrow {AC}}\right)=\\&=&{\overrightarrow {AB}}+\mu \left({\overrightarrow {BA}}+{\dfrac {c}{a+c}}\,\left({\overrightarrow {AB}}+{\overrightarrow {BC}}\right)\right)=\left(1-\mu +{\dfrac {\mu c}{a+c}}\right){\overrightarrow {AB}}+{\dfrac {\mu c}{a+c}}\,{\overrightarrow {BC}}\end{array}}\right.}$ Ahora, dada la independencia lineal de los vectores ${\displaystyle {\overrightarrow {AB}}}$ y ${\displaystyle {\overrightarrow {BC}}}$ entonces: ${\displaystyle \left\{{\begin{array}{rcl}\lambda &=&1-\mu +{\dfrac {\mu c}{a+c}}\\{\dfrac {\lambda c}{b+c}}&=&{\dfrac {\mu c}{a+c}}\end{array}}\right.}$ El sistema anterior, que es un sistema lineal, tiene las soluciones ${\displaystyle \lambda ={\dfrac {b+c}{a+b+c}}\qquad \mu ={\dfrac {a+c}{a+b+c}}}$ Finalmente, ${\displaystyle {\begin{array}{rcl}{\overrightarrow {I}}&=&{\overrightarrow {A}}+{\overrightarrow {AI}}={\overrightarrow {A}}+\lambda {\overrightarrow {AB}}+{\dfrac {\lambda c}{b+c}}\,{\overrightarrow {BC}}={\overrightarrow {A}}+\lambda \left({\overrightarrow {B}}-{\overrightarrow {A}}\right)+{\dfrac {\lambda c}{b+c}}\,\left({\overrightarrow {C}}-{\overrightarrow {B}}\right)=\\&=&{\overrightarrow {A}}+{\dfrac {b+c}{a+b+c}}\left({\overrightarrow {B}}-{\overrightarrow {A}}\right)+{\dfrac {c}{a+b+c}}\,\left({\overrightarrow {C}}-{\overrightarrow {B}}\right)=\\&=&{\dfrac {a}{a+b+c}}\,{\vec {A}}+{\dfrac {b}{a+b+c}}\,{\vec {B}}+{\dfrac {c}{a+b+c}}\,{\vec {C}}\end{array}}}$

Coordenadas trilineales

Las coordenadas trilineales del incentro son

${\displaystyle 1:1:1}$

La colección de centros del triángulo presenta estructura de grupo cuando se expresan sus coordenadas en el sistema trilineal respecto a la operación producto. En este grupo, el incentro es el elemento identidad.^[3]​

Coordenadas baricéntricas

Las coordenadas baricéntricas del incentro son

${\displaystyle \ a:b:c}$

donde ${\displaystyle a}$, ${\displaystyle b}$, y ${\displaystyle c}$ son las longitudes de los lados del triángulo, o de forma equivalente (utilizando el teorema de los senos) se pueden definir como

${\displaystyle \operatorname {sen}(A):\operatorname {sen}(B):\operatorname {sen}(C)}$

donde ${\displaystyle A}$, ${\displaystyle B}$, y ${\displaystyle C}$ son los ángulos de los tres vértices del triángulo.

1	2	3	4
5	6	7	8
9	10	11	12
13	14	15	16

Propiedades del incentro

Distancias a los vértices

Denominando al incentro del triángulo ABC como I, las distancias desde el incentro a los vértices, de acuerdo con las longitudes de los lados, obedecen a la ecuación^[4]​

${\displaystyle {\frac {IA\cdot IA}{CA\cdot AB}}+{\frac {IB\cdot IB}{AB\cdot BC}}+{\frac {IC\cdot IC}{BC\cdot CA}}=1}$

Adicionalmente,^[5]​

${\displaystyle IA\cdot IB\cdot IC=4Rr^{2}}$

donde R y r son los radios de las circunferencias circunscrita e inscrita respectivamente.

Distancia al vértice A.

1. Conociendo el ángulo A y el radio r

${\displaystyle d(I,A)=r\cdot csc{\frac {A}{2}}}$ → (1),^[6]​ r radio de la circunferencia inscrita.

2. Conociendo los tres lados.

${\displaystyle d(I,A)={\sqrt {\frac {bc(p-a)}{p}}}}$ donde a, b y c son las longitudes de los lados y ${\displaystyle p={\frac {a+b+c}{2}}}$ es el semiperímetro.

Para deducir esta fórmula cíclica, se iguala pr con la fórmula de Herón. Se despeja cos A de la fórmula que brinda la ley de los cosenos y se halla el sen de A/2, también el cosecante de A/2. Se reemplaza r y csc A/2 en la fórmula anterior (1).^[7]​

Otros centros

La distancia entre el incentro y el centroide es menor que una tercera parte de la longitud de la mediana más larga del triángulo.^[8]​

De acuerdo con el Teorema geométrico de Euler, la distancia entre el incentro I y el circuncentro O elevada al cuadrado, viene dada por^[9]​^[10]​

${\displaystyle OI^{2}=R(R-2r),}$

donde R y r son el circunradio y el inradio respectivamente; en consecuencia, el circunradio es al menos dos veces el inradio (siendo exactamente el doble únicamente en el caso del triángulo equilátero^[11]​^{: p. 198}).

La distancia desde el incentro al centro N de la circunferencia de los nueve puntos es^[10]​

${\displaystyle IN={\frac {1}{2}}(R-2r)<{\frac {1}{2}}R}$

La distancia al cuadrado entre el incentro y el ortocentro H es^[12]​

${\displaystyle IH^{2}=2r^{2}-4R^{2}\cos A\cos B\cos C}$

Existen inecuaciones que afirman que:

${\displaystyle IG<HG,\quad IH<HG,\quad IG<IO,\quad 2IN<IO}$

El incentro es el punto de Nagel del triángulo medial (el triángulo cuyos vértices son los puntos medios de los lados) y se halla situado en el interior de este triángulo. Recíprocamente, el punto de Nagel de cualquier triángulo es el incentro de su triángulo anticomplementario.^[13]​

El incentro se localiza en el interior de un disco cuyo diámetro une el centroide G y el ortocentro H (el disco ortocentroidal), pero no puede coincidir con el centro de los nueve puntos, cuya posición es fija a 1/4 a lo largo del diámetro (más cercano a G). Ningún otro punto dentro del disco ortocentroidal es el incentro de alguno de los triángulos singulares.^[14]​

Recta de Euler

La recta de Euler de un triángulo pasa a través de su circuncentro, su centroide, y su ortocentro, además de por otros puntos notables. El incentro generalmente no pertenece a la recta de Euler;^[15]​ salvo para los triángulos isósceles,^[16]​ en cuyo caso la recta de Euler coincide con el eje de simetría del triángulo y contiene todos sus centros.

Denominando a la distancia desde el incentro a la recta de Euler d; a la longitud de la mayor mediana v; a la longitud del mayor lado del triángulo u; al circunradio R; a la longitud del segmento de la recta de Euler desde el ortocentro hasta el circuncentro e; y al semiperímetro s; se tienen las inecuaciones siguientes:^[17]​

${\displaystyle {\frac {d}{s}}<{\frac {d}{u}}<{\frac {d}{v}}<{\frac {1}{3}}}$

${\displaystyle d<{\frac {1}{3}}e}$

${\displaystyle d<{\frac {1}{2}}R}$

Divisiones de área y de perímetro

Cualquier recta que divida un triángulo en dos partes de igual área e igual perímetro (ambas condiciones se dan simultáneamente), pasa por su incentro. Puede haber una, dos o tres de estas líneas para cualquier triángulo dado.^[18]​

Distancia relativa de los puntos de una bisectriz

Sea X un punto de la bisectriz del ángulo A. Entonces, cuando X = I (el incentro) se maximiza o minimiza el cociente ${\displaystyle {\tfrac {BX}{CX}}}$ a lo largo de la bisectriz.^[19]​^[20]​

Véase también

• Recta de Euler
• Ortocentro
• Baricentro
• Circuncentro
• Exincentro

Referencias

Enlaces externos

• Weisstein, Eric W. «Incenter». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Encyclopedia of Triangle Centers
• Empresa de Transformación Digital - Incentro