Egybevágósági transzformáció

Egybevágósági transzformációnak (továbbiakban röviden egybevágóságnak) nevezzük a tér önmagára vonatkozó kölcsönösen egyértelmű leképezését, amely a szakaszokat velük egybevágó szakaszokba viszi.[1]

A tér egybevágóságai a kompozíció[2] műveletével csoportot alkotnak. Ez a csoport nem kommutatív. A műveletet jobbról balra végezzük el, azaz pl ha T egy tengelyes tükrözés, F pedig egy forgatás, akkor TF esetén előbb a forgatást végezzük el, és csak aztán a tükrözést.

A síkbeli egybevágóságok tulajdonságai

Tétel
Az egybevágóság egyenestartó transzformáció.[3]
Bizonyítás
A, B, C legyenek egy egyenes három különböző pontja, ebben a sorrendben, ekkor A B ¯ + B C ¯ = A C ¯ {\displaystyle {\overline {AB}}+{\overline {BC}}={\overline {AC}}} . Indirekt tegyük fel, hogy a T egybevágóság ezt a három pontot olyan A', B', C' pontokba viszi, amelyek nem egy egyenesen vannak, tehát egy háromszög csúcspontjai. Mivel T egybevágóság, ezért az A ′ B ′ ¯ + B ′ C ′ ¯ = A ′ C ′ ¯ {\displaystyle {\overline {A'B'}}+{\overline {B'C'}}={\overline {A'C'}}} egyenletnek teljesülnie kell. Viszont mivel A', B', C' egy háromszög három csúcsa, az oldalaira igaz a háromszög-egyenlőtlenség: A ′ B ′ ¯ + B ′ C ′ ¯ > A ′ C ′ ¯ {\displaystyle {\overline {A'B'}}+{\overline {B'C'}}>{\overline {A'C'}}} , ami ellentmondás, mert nyilván nem lehet, hogy két mennyiség egyenlő, ugyanakkor az egyik nagyobb mint a másik. Tehát az indirekt feltevés hamis, vagyis igaz az állítás.
Tétel
Ha egy egybevágóságnak létezik 2 (különböző) fix pontja,[4] akkor a két pontot összekötő egyenes minden pontja fix.
Bizonyítás
Legyen A, B a két különböző fix pont, e pedig az általuk meghatározott egyenes. Legyen P egy, az A-tól és a B-től különböző pontja e-nek. Indirekt tegyük fel, hogy P' (P képe) egy P-től különböző pontja az egyenesnek.[5] Mivel egybevágóságról van szó: P A ¯ = P ′ A ¯ P B ¯ = P ′ B ¯ {\displaystyle {\overline {PA}}={\overline {P'A}}\quad {\overline {PB}}={\overline {P'B}}} teljesülnek, azaz A és B rajta vannak a PP' felező merőlegesén. Mivel azonban az e-n is rajta vannak, és a felező merőleges csak egy pontban metsz e-t: A = B {\displaystyle A=B} , ami ellentmondás, tehát e minden pontja fix.
Tétel
Ha egy egybevágóságnak létezik 3 nem kollineáris[6] fix pontja, akkor a sík minden pontja fix, azaz az egybevágóság identitása a síknak.
Bizonyítás
Legyenek A, B, C a fix pontok. Ekkor az általuk alkotott háromszög mindhárom oldalegyenese fix. Vegyünk fel egy tetszőleges Ppontot a síkon, és legyen Q az egyik oldalegyenes belső pontja. A Pasch-axióma[7] miatt létezik olyan R pont, hogy a PQ egyenes R-ben metszi egy másik egyenes belső pontját. Mivel Q, R fix pontok (az oldalegyenesek minden pontja fix), az RQ egyenesnek is minden pontja fix, tehát P is az.

Az eddigi tételek igazak a térben is, a következőkben viszont szigorúan egysíkúak leszünk.

Tengelyes tükrözés

Tengelyes tükrözés
A síknak egy adott t egyenesre való tükrözése az a leképezés, amely egy tetszőleges P ponthoz azt a P' pontot rendeli képként, amelyre igaz, hogy P P ′ ⊥ t {\displaystyle PP'\perp t} és P P ′ ∩ t {\displaystyle PP'\cap t} -t T-vel jelölve P T ≅ P ′ T {\displaystyle PT\cong P'T} A t egyenes pontjai fixek. A tükrözést a tengellyel lehet jellemezni. Kétszer egymás után ugyanarra az egyenesre tükrözés az identitás (azaz: t ⋅ t = t 2 = 1 ⇔ t − 1 = t ) {\displaystyle t\cdot t=t^{2}=1\Leftrightarrow t^{-1}=t)}
Tétel
Az egyenesre vonatkozó tükrözés egybevágóság.
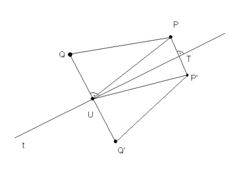
Bizonyítás
Δ P T U ≅ Δ P ′ T U {\displaystyle \Delta _{PTU}\cong \Delta _{P'TU}} mivel a TU oldal közös, P T ≅ P ′ T {\displaystyle PT\cong P'T} és a PTU szög egyenlő a P'TUszöggel. Ebből következik, hogy P U ¯ ≅ P ′ U ¯ {\displaystyle {\overline {PU}}\cong {\overline {P'U}}} és PUT szög egyenlő P'UT szöggel, tehát QUP szög egyenlő Q'UP' szöggel. Ezekből: Δ P U Q ≅ Δ P ′ U Q ′ ⇒ P Q ¯ ≅ P ′ Q ′ ¯ {\displaystyle \Delta _{PUQ}\cong \Delta _{P'UQ'}\Rightarrow {\overline {PQ}}\cong {\overline {P'Q'}}}
Tétel
Ha a sík egy identitástól különböző T egybevágóságnak van két fix pontja, akkor T a fixpontokat összekötő egyenesre való tengelyes tükrözés.
Bizonyítás
Legyen t a két fix ponton (A-n és B-n) áthaladó egyenes. Ekkor t minden pontja fix, és tetszőleges t-n kívüli P pont nem lehet fix (ld: előző tételek), tehát P' különbözik P-től. Mivel T egy egybevágóság: P A ¯ = P ′ A ¯ P B ¯ = P ′ B ¯ {\displaystyle {\overline {PA}}={\overline {P'A}}\quad {\overline {PB}}={\overline {P'B}}} tehát t a PP' szakasz felező merőlegese. Azaz: P P ′ ⊥ t P T ¯ ≅ P ′ T ¯ ⇒ {\displaystyle PP'\perp t\quad {\overline {PT}}\cong {\overline {P'T}}\Rightarrow } P' a P pont tükörképe t-re
Tétel
Ha a sík egy F egybevágóságának pontosan 1 fix pontja van, akkor F előáll két tengelyes tükrözés kompozíciójaként, melyek tengelyei áthaladnak a fixponton.
Bizonyítás
Legyen A a fix pont. Ekkor tetszőleges A-tól különböző P esetén P' különbözik P-től. Legyen t a PP' felezőmerőlegese. A rajta van t-n, mert P A ¯ ≅ P ′ A ¯ {\displaystyle {\overline {PA}}\cong {\overline {P'A}}} (ugyanis F egybevágóság). Tehát a tF egybevágóságnak A fix pontja és P is önmagára képzödik (ugyanis: P ⟼ F P ′ ⟼ t P ) {\displaystyle P\longmapsto ^{\mathbf {F} }P'\longmapsto ^{t}P)} Tehát A és P két fix pontja a tF egybevágóságnak ⇒ t F = s ⇒ F = t s {\displaystyle \Rightarrow t\mathbf {F} =s\Rightarrow \mathbf {F} =ts}

Jegyzetek

  1. ↑ A síkbeli egybevágóságok olyan térbeli egybevágóságok, amelyek az adott síkot önmagára képezik.
  2. ↑ A függvények egymás után való alkalmazása.
  3. ↑ Olyan transzformáció, amelyre igaz, hogy az egyenes minden pontjára alkalmazva a pontok képe egyenes.
  4. ↑ Olyan pont, amit az egybevágóság önmagába visz
  5. ↑ Az előző tétel miatt biztos, hogy az egyenesen van rajta
  6. ↑ Nem egy egyenesen lévő
  7. ↑ ld: Hilbert-féle axiómarendszer#A rendezés axiómái 4. pont

Lásd még

  • Transzformáció