グローバーのアルゴリズム とは、N 個の要素をもつ未整序 データベース の中から指定された値を検索する探索 問題を解くための量子コンピュータ のアルゴリズム であり、O(N1/2 ) のオーダーの計算量 と、O( logN) のオーダー(ランダウの記号 も参照)の記憶領域を消費する。1996年 にロブ・グローバー(英語版) によって開発された。
概要 典型的には、未整序データベースからの探索は、O(N) の計算時間を要する線型探索 を用いなければならない。グローバーのアルゴリズムは、O(N1/2 ) の計算時間しか消費せず、未整序データベース探索を行う量子アルゴリズムの中で最も速い[1]
このアルゴリズムは他の量子アルゴリズムがしばしば、古典アルゴリズム と比較して指数 的な速度向上をもたらすのとは異なり、二次の速度向上しかもたらさない。しかし、N が大きければ、二次の向上でもかなりの向上となる。たとえば、グローバーのアルゴリズムを共通鍵暗号の総当り攻撃に利用すると、128ビット鍵であれば264 の繰り返しで、256ビット鍵であれば2128 の繰り返しで求めることができる。このため、将来の量子総当り攻撃に対して安全性を持たせるために、鍵長を2倍にすることが提案されている[2]
他の量子アルゴリズムと同じように、グローバーのアルゴリズムは正しい解を高い確率 で与える確率的アルゴリズム である。この解が正しくない確率は、このアルゴリズムを繰り返すことによって減少させることができる(確率的アルゴリズムでない、正しい確率が1の解を与える、決定的アルゴリズム についてはドイッチュ・ジョサのアルゴリズム を参照)。
応用 グローバーのアルゴリズムの目的は普通「データベース探索」とされるが、「逆関数の導出」と言うとより正確かもしれない。おおざっぱにいうと、y=f(x) という量子コンピュータで処理できる関数があったとして、このアルゴリズムを使うとあるy を与えるx の値を計算することができる。データベース探索は、データベースをインデックスx に対してデータy を与える関数と考えれば、逆関数を求めることと同値である。
グローバーのアルゴリズムは、平均 と中央値 を推定すること、また衝突問題(w:Collision problem)を解くのにも使える。また、可能性のある解を総当たりで探すことによってNP完全 問題を解くことにも使える。これは、膨大な可能性を試すのに、重ね合わせを用いることで限られた計算量しか消費しないので、古典アルゴリズムに比べてかなりのスピードアップを見込めるが、指数時間かかってしまうことは変らない。あらかじめ解が複数あることとその個数がわかっている場合、このアルゴリズムはさらに高速化することができる。
準備 N個のデータを持つデータベースを考える。データベースの中から、何らかの検索条件を満たすデータを探し出す問題を考えよう。 グローバーのアルゴリズムは、 N {\displaystyle N} 状態空間 H {\displaystyle {\mathcal {H}}} n = ⌈ log 2 N ⌉ {\displaystyle n=\lceil \log _{2}N\rceil } 量子ビット あれば満され、基底状態は
| 1 ⟩ , | 2 ⟩ , … , | N ⟩ {\displaystyle |1\rangle ,|2\rangle ,\ldots ,|N\rangle } と書ける。これらの固有値 { λ 1 , λ 2 , ⋯ , λ N } {\displaystyle \{\lambda _{1},\lambda _{2},\cdots ,\lambda _{N}\}}
f {\displaystyle f} x ∈ { 1 , 2 , … , N } {\displaystyle x\in \{1,2,\ldots ,N\}} v {\displaystyle v} D [ x ] = v {\displaystyle D[x]=v} x {\displaystyle x}
{ f ( x ) = 1 if D [ x ] = v , f ( x ) = 0 if D [ x ] ≠ v {\displaystyle {\begin{cases}f(x)=1&{\text{ if }}D[x]=v,\\f(x)=0&{\text{ if }}D[x]\neq v\end{cases}}} である。以下では ω {\displaystyle \omega } f ( ω ) = 1 {\displaystyle f(\omega )=1} ユニタリ演算子 U ω {\displaystyle U_{\omega }} サブルーチン として使えるとする。(このサブルーチンは、オラクル とも呼ばれる。)
{ U ω | x ⟩ = − | x ⟩ for x = ω , that is f ( x ) = 1 U ω | x ⟩ = | x ⟩ for x ≠ ω , that is f ( x ) = 0 {\displaystyle {\begin{cases}U_{\omega }|x\rangle =-|x\rangle &{\text{for }}x=\omega {\text{, that is }}f(x)=1\\U_{\omega }|x\rangle =|x\rangle &{\text{for }}x\neq \omega {\text{, that is }}f(x)=0\end{cases}}} アルゴリズムの目的は、インデクス | ω ⟩ {\displaystyle |\omega \rangle }
なお、(下に示す量子回路のように)補助量子ビットシステムを使う場合には、演算子 U ω {\displaystyle U_{\omega }} f ( x ) {\displaystyle f(x)}
{ U ω | x ⟩ | y ⟩ = | x ⟩ | ¬ y ⟩ for x = ω , that is f ( x ) = 1 , U ω | x ⟩ | y ⟩ = | x ⟩ | y ⟩ for x ≠ ω , that is f ( x ) = 0 , {\displaystyle {\begin{cases}U_{\omega }|x\rangle |y\rangle =|x\rangle |\neg y\rangle &{\text{for }}x=\omega {\text{, that is }}f(x)=1,\\U_{\omega }|x\rangle |y\rangle =|x\rangle |y\rangle &{\text{for }}x\neq \omega {\text{, that is }}f(x)=0,\end{cases}}} あるいは、
U ω | x ⟩ | y ⟩ = | x ⟩ | y ⊕ f ( x ) ⟩ . {\displaystyle U_{\omega }|x\rangle |y\rangle =|x\rangle |y\oplus f(x)\rangle .} で表現される。
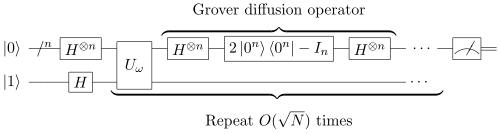
アルゴリズムの流れ グローバーのアルゴリズムを表す量子回路 | s ⟩ {\displaystyle |s\rangle }
| s ⟩ = 1 N ∑ x = 0 N − 1 | x ⟩ {\displaystyle |s\rangle ={\frac {1}{\sqrt {N}}}\sum _{x=0}^{N-1}|x\rangle } とし、演算子 U s {\displaystyle U_{s}}
U s = 2 | s ⟩ ⟨ s | − I {\displaystyle U_{s}=2\left|s\right\rangle \left\langle s\right|-I} とする。この演算子は、グローバーの拡散演算子と呼ばれている。
グローバーのアルゴリズムの流れは以下の通りである。
初期状態を以下の様に用意する: | s ⟩ = 1 N ∑ x = 1 N | x ⟩ {\displaystyle |s\rangle ={\frac {1}{\sqrt {N}}}\sum _{x=1}^{N}|x\rangle } 次にしめす"Grover iteration"を r ( N ) {\displaystyle r(N)} r ( N ) {\displaystyle r(N)} O ( N ) {\displaystyle O({\sqrt {N}})} 演算子 U ω {\displaystyle U_{\omega }} 演算子 U s {\displaystyle U_{s}} 状態Ω を観測する。観測の結果は、Nが十分に大きければ、1に近い確率でλω となり、 ω {\displaystyle \omega } 1回目の繰り返し 演算子 U s {\displaystyle U_{s}}
U s = 2 | s ⟩ ⟨ s | − I , {\displaystyle U_{s}=2|s\rangle \langle s|-I,} で定義されており、さらに、演算子 U ω {\displaystyle U_{\omega }}
U ω = I − 2 | ω ⟩ ⟨ ω | {\displaystyle U_{\omega }=I-2|\omega \rangle \langle \omega |} これを確認するには、 I − 2 | ω ⟩ ⟨ ω | {\displaystyle I-2|\omega \rangle \langle \omega |}
( I − 2 | ω ⟩ ⟨ ω | ) | ω ⟩ = | ω ⟩ − 2 | ω ⟩ ⟨ ω | ω ⟩ = − | ω ⟩ = U ω | ω ⟩ ( I − 2 | ω ⟩ ⟨ ω | ) | x ⟩ = | x ⟩ − 2 | ω ⟩ ⟨ ω | x ⟩ = | x ⟩ = U ω | x ⟩ ∀ x ≠ ω {\displaystyle {\begin{aligned}(I-2|\omega \rangle \langle \omega |)|\omega \rangle &=|\omega \rangle -2|\omega \rangle \langle \omega |\omega \rangle =-|\omega \rangle =U_{\omega }|\omega \rangle \\(I-2|\omega \rangle \langle \omega |)|x\rangle &=|x\rangle -2|\omega \rangle \langle \omega |x\rangle =|x\rangle =U_{\omega }|x\rangle &&\forall x\neq \omega \end{aligned}}} さらに、 | ω ⟩ {\displaystyle |\omega \rangle } | s ⟩ {\displaystyle |s\rangle }
⟨ ω | s ⟩ = ⟨ s | ω ⟩ = 1 N , ⟨ s | s ⟩ = N 1 N ⋅ 1 N = 1 {\displaystyle {\begin{aligned}\langle \omega |s\rangle &=\langle s|\omega \rangle ={\tfrac {1}{\sqrt {N}}},\\\langle s|s\rangle &=N{\tfrac {1}{\sqrt {N}}}\cdot {\tfrac {1}{\sqrt {N}}}=1\end{aligned}}} が成り立つ。したがって、1回目の繰り返しでは次にように計算される。
U ω | s ⟩ = ( I − 2 | ω ⟩ ⟨ ω | ) | s ⟩ = | s ⟩ − 2 | ω ⟩ ⟨ ω | s ⟩ = | s ⟩ − 2 N | ω ⟩ , U s ( | s ⟩ − 2 N | ω ⟩ ) = ( 2 | s ⟩ ⟨ s | − I ) ( | s ⟩ − 2 N | ω ⟩ ) = 2 | s ⟩ ⟨ s | s ⟩ − | s ⟩ − 4 N | s ⟩ ⟨ s | ω ⟩ + 2 N | ω ⟩ = 2 | s ⟩ − | s ⟩ − 4 N ⋅ 1 N | s ⟩ + 2 N | ω ⟩ = N − 4 N | s ⟩ + 2 N | ω ⟩ . {\displaystyle {\begin{aligned}U_{\omega }|s\rangle &=(I-2|\omega \rangle \langle \omega |)|s\rangle =|s\rangle -2|\omega \rangle \langle \omega |s\rangle =|s\rangle -{\tfrac {2}{\sqrt {N}}}|\omega \rangle ,\\U_{s}\left(|s\rangle -{\tfrac {2}{\sqrt {N}}}|\omega \rangle \right)&=\left(2|s\rangle \langle s|-I\right)\left(|s\rangle -{\tfrac {2}{\sqrt {N}}}|\omega \rangle \right)=2|s\rangle \langle s|s\rangle -|s\rangle -{\tfrac {4}{\sqrt {N}}}|s\rangle \langle s|\omega \rangle +{\tfrac {2}{\sqrt {N}}}|\omega \rangle \\&=2|s\rangle -|s\rangle -{\tfrac {4}{\sqrt {N}}}\cdot {\tfrac {1}{\sqrt {N}}}|s\rangle +{\tfrac {2}{\sqrt {N}}}|\omega \rangle \\&={\tfrac {N-4}{N}}|s\rangle +{\tfrac {2}{\sqrt {N}}}|\omega \rangle .\end{aligned}}} 分かりやすい例として、 N {\displaystyle N} f ( ω ) = 1 {\displaystyle f(\omega )=1} ω {\displaystyle \omega } U s U w | s ⟩ = | ω ⟩ {\displaystyle U_{s}U_{w}|s\rangle =|\omega \rangle }
一般の場合では、 U ω {\displaystyle U_{\omega }} U s {\displaystyle U_{s}} | ⟨ ω | s ⟩ | 2 = 1 N {\displaystyle \left|\langle \omega |s\rangle \right|^{2}={\tfrac {1}{N}}} | ⟨ ω | U s U ω | s ⟩ | 2 = | 1 N ⋅ N − 4 N + 2 N | 2 = ( 3 N − 4 ) 2 N 3 = 9 ( 1 − 4 3 N ) 2 ⋅ 1 N {\displaystyle \left|\langle \omega |U_{s}U_{\omega }|s\rangle \right|^{2}=\left|{\tfrac {1}{\sqrt {N}}}\cdot {\tfrac {N-4}{N}}+{\tfrac {2}{\sqrt {N}}}\right|^{2}={\tfrac {(3N-4)^{2}}{N^{3}}}=9\left(1-{\tfrac {4}{3N}}\right)^{2}\cdot {\tfrac {1}{N}}}
妥当性の幾何学的な証明 グローバーのアルゴリズムの最初の繰り返しの幾何学的な解釈。状態ベクトル | s ⟩ {\displaystyle |s\rangle } | ω ⟩ {\displaystyle |\omega \rangle } |s >と|ω >で張られる空間を考える。この平面は、 | ω ⟩ {\displaystyle |\omega \rangle } | s ′ ⟩ = 1 N − 1 ∑ x ≠ ω | x ⟩ {\displaystyle \textstyle |s'\rangle ={\frac {1}{\sqrt {N-1}}}\sum _{x\neq \omega }|x\rangle } | s ⟩ {\displaystyle |s\rangle } | ω ⟩ {\displaystyle |\omega \rangle } | s ⟩ {\displaystyle |s\rangle } | s ′ ⟩ {\displaystyle |s'\rangle }
⟨ s ′ | s ⟩ = N − 1 N {\displaystyle \langle s'|s\rangle ={\sqrt {\frac {N-1}{N}}}} 幾何学 的に言えば、 | s ⟩ {\displaystyle |s\rangle } | s ′ ⟩ {\displaystyle |s'\rangle } θ / 2 {\displaystyle \theta /2}
sin θ 2 = 1 N {\displaystyle \sin {\frac {\theta }{2}}={\frac {1}{\sqrt {N}}}} 演算子Uω は、|s >と|ω >で張られる空間を、|ω >と垂直 な超平面 を対称面として反転 させる。つまり、空間上のベクトルを、 | s ′ ⟩ {\displaystyle |s'\rangle } Us は、|s >を対称面とする反転である。よって、|s >と|ω >によって張られる平面上にあるベクトルは、Us とUω で演算されても、その平面上に留まる。また、Grover iterationUs Uω の各繰り返しで、状態ベクトルは |ω > に向かって角度 θ = 2 arcsin 1 N ≈ 2 1 N {\displaystyle \theta =2\arcsin {\tfrac {1}{\sqrt {N}}}\approx 2{\tfrac {1}{\sqrt {N}}}}
状態ベクトルが|ω >に近付いたなら、繰返しを止めなければならない。繰返しを重ねすぎると、状態ベクトルは|ω >から離れていってしまい、正しい解を与える確率を下げてしまう。 r {\displaystyle r}
sin 2 ( ( r + 1 2 ) θ ) {\displaystyle \sin ^{2}\left({\Big (}r+{\frac {1}{2}}{\Big )}\theta \right)} である。したがって、ほぼ最適な測定が得られる繰り返し回数は r ≈ π N / 4 {\displaystyle r\approx \pi {\sqrt {N}}/4}
妥当性の代数的な証明 代数的な解析をするには、 U s U ω {\displaystyle U_{s}U_{\omega }} s {\displaystyle s} ω {\displaystyle \omega } { | s ⟩ , | ω ⟩ } {\displaystyle \{|s\rangle ,|\omega \rangle \}} U s {\displaystyle U_{s}} U ω {\displaystyle U_{\omega }}
U s : a | ω ⟩ + b | s ⟩ ↦ [ | ω ⟩ | s ⟩ ] [ − 1 0 2 / N 1 ] [ a b ] {\displaystyle U_{s}:a|\omega \rangle +b|s\rangle \mapsto [|\omega \rangle \,|s\rangle ]{\begin{bmatrix}-1&0\\2/{\sqrt {N}}&1\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}} U ω : a | ω ⟩ + b | s ⟩ ↦ [ | ω ⟩ | s ⟩ ] [ − 1 − 2 / N 0 1 ] [ a b ] {\displaystyle U_{\omega }:a|\omega \rangle +b|s\rangle \mapsto [|\omega \rangle \,|s\rangle ]{\begin{bmatrix}-1&-2/{\sqrt {N}}\\0&1\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}} よって、 { | ω ⟩ , | s ⟩ } {\displaystyle \{|\omega \rangle ,|s\rangle \}} U ω {\displaystyle U_{\omega }} U s {\displaystyle U_{s}} U s U ω {\displaystyle U_{s}U_{\omega }}
U s U ω = [ − 1 0 2 / N 1 ] [ − 1 − 2 / N 0 1 ] = [ 1 2 / N − 2 / N 1 − 4 / N ] {\displaystyle U_{s}U_{\omega }={\begin{bmatrix}-1&0\\2/{\sqrt {N}}&1\end{bmatrix}}{\begin{bmatrix}-1&-2/{\sqrt {N}}\\0&1\end{bmatrix}}={\begin{bmatrix}1&2/{\sqrt {N}}\\-2/{\sqrt {N}}&1-4/N\end{bmatrix}}} この行列は、非常に便利なジョルダン標準形 をしている。 t = arcsin ( 1 / N ) {\displaystyle t=\arcsin(1/{\sqrt {N}})}
U s U ω = M [ exp ( 2 i t ) 0 0 exp ( − 2 i t ) ] M − 1 {\displaystyle U_{s}U_{\omega }=M{\begin{bmatrix}\exp(2it)&0\\0&\exp(-2it)\end{bmatrix}}M^{-1}} M = [ − i i exp ( i t ) exp ( − i t ) ] {\displaystyle M={\begin{bmatrix}-i&i\\\exp(it)&\exp(-it)\end{bmatrix}}} と書ける。 これにより、この行列の r 乗(r 回の繰り返しに対応する)は、
( U s U ω ) r = M [ exp ( 2 r i t ) 0 0 exp ( − 2 r i t ) ] M − 1 {\displaystyle (U_{s}U_{\omega })^{r}=M{\begin{bmatrix}\exp(2rit)&0\\0&\exp(-2rit)\end{bmatrix}}M^{-1}} となる。この形式を使えば、三角関数の公式を使って、r 回の繰り返しの後に目的の ω {\displaystyle \omega }
| [ ⟨ ω | ω ⟩ ⟨ ω | s ⟩ ] ( U s U ω ) r [ 0 1 ] | 2 = sin 2 ( ( 2 r + 1 ) t ) {\displaystyle \left|{\begin{bmatrix}\langle \omega |\omega \rangle &\langle \omega |s\rangle \end{bmatrix}}(U_{s}U_{\omega })^{r}{\begin{bmatrix}0\\1\end{bmatrix}}\right|^{2}=\sin ^{2}\left((2r+1)t\right)} と計算することができる。(幾何学的な解析で得た確率と同じ。)
あるいは、最適な繰り返し回数は、角度 2 r t {\displaystyle 2rt} − 2 r t {\displaystyle -2rt} 2 r t ≈ π / 2 {\displaystyle 2rt\approx \pi /2} r = π / 4 t = π / 4 arcsin ( 1 / N ) ≈ π N / 4 {\displaystyle r=\pi /4t=\pi /4\arcsin(1/{\sqrt {N}})\approx \pi {\sqrt {N}}/4}
[ | ω ⟩ | s ⟩ ] ( U s U ω ) r [ 0 1 ] ≈ [ | ω ⟩ | s ⟩ ] M [ i 0 0 − i ] M − 1 [ 0 1 ] = | ω ⟩ 1 cos ( t ) − | s ⟩ sin ( t ) cos ( t ) {\displaystyle [|\omega \rangle \,|s\rangle ](U_{s}U_{\omega })^{r}{\begin{bmatrix}0\\1\end{bmatrix}}\approx [|\omega \rangle \,|s\rangle ]M{\begin{bmatrix}i&0\\0&-i\end{bmatrix}}M^{-1}{\begin{bmatrix}0\\1\end{bmatrix}}=|\omega \rangle {\frac {1}{\cos(t)}}-|s\rangle {\frac {\sin(t)}{\cos(t)}}} の状態で終了する。 少し計算すれば、観測によって(エラー確率 O (1/N ) を除き)正しい答え ω {\displaystyle \omega }
発展形 もし、探索条件にあうデータが1個だけでなく、k 個存在するならば、同じアルゴリズムを適用できるが、繰返し回数はπN1/2 /4 の代わりにπ(N/k)1/2 /4 としなければならない。 k が未知の場合を取り扱う方法は幾つかある。例として、繰返し回数を以下のようにしてグローバーのアルゴリズムを何回か走らせる方法がある。
π N 1 / 2 4 , π ( N / 2 ) 1 / 2 4 , π ( N / 4 ) 1 / 2 4 , … {\displaystyle \pi {\frac {N^{1/2}}{4}},\pi {\frac {(N/2)^{1/2}}{4}},\pi {\frac {(N/4)^{1/2}}{4}},\ldots }
k がどのような値でも、上のような繰返し回数で行えば正しい解を高い確率で得られる。繰返しの総回数は多くとも次のようであり、O(N1/2 )のオーダーにとどまる。
π N 1 / 2 4 ( 1 + 1 2 + 1 2 + ⋯ ) {\displaystyle \pi {\frac {N^{1/2}}{4}}\left(1+{\frac {1}{\sqrt {2}}}+{\frac {1}{2}}+\cdots \right)}
このアルゴリズムは改良の余地がある。k が未知であるとして、 O ( N k ) 1 / 2 {\displaystyle O({\frac {N}{k}})^{1/2}}
最適性 グローバーのアルゴリズムは最適であることが知られている。つまり、データベースにUω のみを用いてアクセスするようなどんなアルゴリズムも、グローバーのアルゴリズムと同じかそれ以上の回数だけUω を作用させなければならない[1] c N 回Uω 適用することで解くことができるとすれば、NP 問題をグローバーの探索問題に帰着させることで、NPがBQP に含まれることが示される。グローバーのアルゴリズムが最適であることは、NPはBQPに含まれないことを示唆している(ただし証明しているわけではない)。
k 個の条件に該当するデータがある場合、π(N/k)1/2 /4 も最適である。
適用可能性と制約 このアルゴリズムにおいては、データベースは明示的に表されておらず、代わりに、インデクスによってデータで評価するためにオラクルを呼び出す。データベース全体をデータごとに読み込み、それをインデクスを使って評価できる形式に変換することは、グローバーの検索よりもはるかに時間がかかる場合がある。これを考えると、グローバーのアルゴリズムは、方程式や制約充足問題 を解くための方法であると見ることができる。このようなアプリケーションでは、オラクルは制約を満たすかどうかをチェックする方法であり、検索アルゴリズムとは無関係に動作する。一方、従来の検索アルゴリズムでは、検索アルゴリズムを制約のチェック方法と合わせて考慮することで総当たりを回避して最適化を行うことが良くある。グローバーのアルゴリズムではこれらが分離しているため、アルゴリズムの最適化が妨げられる。グローバーのアルゴリズムの使用に関するこれらおよびその他の考慮事項は、Viamontes、Markov、およびHayesによる論文で説明されている。[3]
関連項目 en:Amplitude amplification 参考文献 Grover L.K.: A fast quantum mechanical algorithm for database search , Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212 Grover L.K.: From Schrödinger's equation to quantum search algorithm , American Journal of Physics, 69(7): 769-777, 2001. Pedagogical review of the algorithm and its history. http://www.bell-labs.com/user/feature/archives/lkgrover/ http://arxiv.org/abs/quant-ph/0301079 Grover's Algorithm: Quantum Database Search Grover's algorithm on arxiv.org 脚注 ^ a b Bennett C.H., Bernstein E., Brassard G., Vazirani U., The strengths and weaknesses of quantum computation . w:SIAM Journal on Computing 26(5): 1510-1523 (1997). Shows the optimality of Grover's algorithm. ^ Daniel J. Bernstein (2010-03-03). Grover vs. McEliece . http://cr.yp.to/codes/grovercode-20100303.pdf . ^ Viamontes G.F.; Markov I.L.; Hayes J.P. (2005), “Is Quantum Search Practical?”, Computing in Science and Engineering 7 (3): 62–70, arXiv:quant-ph/0405001, Bibcode: 2005CSE.....7c..62V, doi:10.1109/mcse.2005.53, https://web.eecs.umich.edu/~imarkov/pubs/jour/cise05-grov.pdf 全般 ハードウェア アルゴリズム• 項目 関連分野 メーカー 実機 人物









![{\displaystyle D[x]=v}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6b122869017b257f0dc293aef98465053d5edaa)

![{\displaystyle {\begin{cases}f(x)=1&{\text{ if }}D[x]=v,\\f(x)=0&{\text{ if }}D[x]\neq v\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc26276e8c6b49894500fc6f3a8234d04e66970b)




































![{\displaystyle U_{s}:a|\omega \rangle +b|s\rangle \mapsto [|\omega \rangle \,|s\rangle ]{\begin{bmatrix}-1&0\\2/{\sqrt {N}}&1\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a0b3150cc02d7e7f3205c63c743d543264c6a7b)
![{\displaystyle U_{\omega }:a|\omega \rangle +b|s\rangle \mapsto [|\omega \rangle \,|s\rangle ]{\begin{bmatrix}-1&-2/{\sqrt {N}}\\0&1\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db5c0718db3b1705bdbd00dc494c2db2c25ebf45)











^{r}{\begin{bmatrix}0\\1\end{bmatrix}}\approx [|\omega \rangle \,|s\rangle ]M{\begin{bmatrix}i&0\\0&-i\end{bmatrix}}M^{-1}{\begin{bmatrix}0\\1\end{bmatrix}}=|\omega \rangle {\frac {1}{\cos(t)}}-|s\rangle {\frac {\sin(t)}{\cos(t)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20f60193e79e9db675395c133e7cd361fc31352b)










