| 完全2部グラフ |
|---|
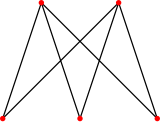 m=3 n =2の完全2部グラフ |
| 頂点 | n+m |
|---|
| 辺 | mn |
|---|
| 自己同型 | 2m!n! if m=n, その他 m!n! |
|---|
| テンプレートを表示 |
完全2部グラフ(かんぜんにぶグラフ、英: complete bipartite graph)は、グラフ理論において、2部グラフのうち特に第1の集合に属するそれぞれの頂点から第2の集合に属する全ての頂点に辺が伸びているものをいう。bicliqueとも。
定義
完全2部グラフ  は2部グラフであり、任意の2つの頂点
は2部グラフであり、任意の2つの頂点  と
と  について
について  内の辺
内の辺  が存在する。完全2部グラフのパーティションの大きさが
が存在する。完全2部グラフのパーティションの大きさが  と
と  であるとき、これを
であるとき、これを  と表記する。
と表記する。
例
- 任意の k について、
 をスターと呼ぶ。木でもある完全2部グラフは、全てスターである。
をスターと呼ぶ。木でもある完全2部グラフは、全てスターである。 - グラフ
 を爪と呼ぶ。
を爪と呼ぶ。 - グラフ
 を utility graph と呼ぶ。
を utility graph と呼ぶ。
 星グラフ S3, S4, S5, S6
星グラフ S3, S4, S5, S6 -
K1,1
-
K2,1
-
K2,2
-
K3,1
-
K3,2
-
K3,3
-
K7,1
特性
- 2部グラフから、辺数
 が最大となる完全2部部分グラフ
が最大となる完全2部部分グラフ  を求める問題は、NP完全問題である。
を求める問題は、NP完全問題である。 - 平面グラフは
 をマイナーとして含むことができない。外平面 (outerplanar) グラフは
をマイナーとして含むことができない。外平面 (outerplanar) グラフは  をマイナーとして含むことができない(これらは平面性や外平面性の十分条件ではないが、必要条件である)。
をマイナーとして含むことができない(これらは平面性や外平面性の十分条件ではないが、必要条件である)。 - 完全2部グラフ
 は
は -cage である。
-cage である。 - 完全2部グラフ
 または
または  は Turán graph である。
は Turán graph である。 - 完全2部グラフ
 の頂点被覆数は
の頂点被覆数は  、辺被覆数は
、辺被覆数は  である。
である。 - 完全2部グラフ
 の最大独立集合の大きさは
の最大独立集合の大きさは  である。
である。 - 完全2部グラフ
 の隣接行列の固有値は
の隣接行列の固有値は  、
、 、0であり、重複度はそれぞれ 1、1、n+m-2 である。
、0であり、重複度はそれぞれ 1、1、n+m-2 である。 - 完全2部グラフ
 のラプラシアン行列の固有値は n+m、n、m、0 であり、重複度はそれぞれ 1、m-1、n-1、1 である。
のラプラシアン行列の固有値は n+m、n、m、0 であり、重複度はそれぞれ 1、m-1、n-1、1 である。 - 完全2部グラフ
 には mn-1 nm-1 の全域木がある。
には mn-1 nm-1 の全域木がある。 - 完全2部グラフ
 には大きさ
には大きさ  の最大マッチングがある。
の最大マッチングがある。 - 完全2部グラフ
 にはラテン方格に対応した n色の辺彩色が存在する。
にはラテン方格に対応した n色の辺彩色が存在する。 - 最後の2つは、k-正則2部グラフに結婚定理を適用することで得られる系である。
関連項目


 K1,1
K1,1 K2,1
K2,1 K2,2
K2,2 K3,1
K3,1 K3,2
K3,2 K3,3
K3,3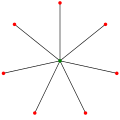 K7,1
K7,1






























