Icosagone

Cet article est une ébauche concernant la géométrie.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Un icosagone est un polygone à 20 sommets, donc 20 côtés et 170 diagonales.

La somme des angles internes d'un icosagone non croisé vaut 3 240 degrés.

L'icosagone régulier est constructible.

Icosagones réguliers

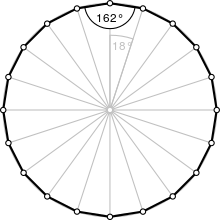
Un icosagone régulier est un icosagone dont les 20 côtés ont même longueur et dont les angles internes ont même mesure. Il y en a quatre : trois étoilés (les icosagrammes notés {20/3}, {20/7} et {20/9}) et un convexe (noté {20}). C'est de ce dernier qu'il s'agit lorsqu'on parle de « l'icosagone régulier ».

• Les trois icosagones réguliers étoilés
• 
  {20/3} (angle interne : 126°)
• 
  {20/7} (angle interne : 54°)
• 
  {20/9} (angle interne : 18°)

Caractéristiques de l'icosagone régulier

Chacun des 20 angles au centre mesure ${\displaystyle {\frac {360^{\circ }}{20}}=18^{\circ }}$ et chaque angle interne mesure ${\displaystyle {\frac {3\,240^{\circ }}{20}}=162^{\circ }}$.

Si a est la longueur d'une arête :

• le périmètre vaut ${\displaystyle P=20\,a}$ ;
• l'aire vaut ${\displaystyle A=5\,a^{2}\cot \left({\frac {\pi }{20}}\right)}$, soit :

${\displaystyle A=5\,a^{2}\left(1+{\sqrt {5}}+{\sqrt {5+2{\sqrt {5}}}}\right)}$^[1] ;

• l'apothème vaut ${\displaystyle H={\frac {2\,A}{P}}={\frac {a}{2}}\cot \left({\frac {\pi }{20}}\right)}$ ;
• le rayon vaut ${\displaystyle R={\frac {H}{\cos \left({\frac {\pi }{20}}\right)}}={\frac {a}{2\sin \left({\frac {\pi }{20}}\right)}}}$.

Constructibilité

On peut construire l'icosagone à partir du décagone (obtenu lui-même d'une façon ou d'une autre), de la même façon qu'on construit ce dernier à partir du pentagone : par bissection.

On pouvait le prévoir grâce au théorème de Gauss-Wantzel, puisque 20 est le produit de 4 (puissance de 2) par 5 (nombre premier de Fermat).

Référence

Voir aussi

Articles connexes

• Expression des lignes trigonométriques pour les premiers multiples de 3° (9° = π/20 rad)
• Svastika (un icosagone simple non régulier et non convexe)

Lien externe

(en) Eric W. Weisstein, « Trigonometry Angles — Pi/20 », sur MathWorld

• Portail de la géométrie