Wzory skróconego mnożenia

Wzory skróconego mnożenia – zestaw tożsamości algebraicznych zawierających potęgi o wykładniku naturalnym oraz dodawanie i odejmowanie; wzory te zawierają wyrażenie algebraiczne takie jak:

• potęgi skończonych sum i różnic: ${\displaystyle (a\pm b)^{n},\ (a_{1}\pm a_{2}\pm \dots \pm a_{k})^{n};}$
• różnice dwóch potęg: ${\displaystyle a^{n}-b^{n},}$
• dla wykładników nieparzystych także sumy takich potęg: ${\displaystyle a^{n}+b^{n}.}$

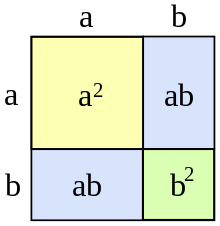
Najprostsze przykłady to te dla wykładnika dwa^[1]:

• kwadrat sumy i różnicy: ${\displaystyle (a\pm b)^{2}=a^{2}\pm 2ab+b^{2};}$
• różnica kwadratów: ${\displaystyle a^{2}-b^{2}=(a-b)(a+b).}$

Wzory te zachodzą dla dowolnych liczb rzeczywistych, zespolonych i wszystkich innych pierścieni przemiennych^{[potrzebny przypis]}, ponieważ wynikają z podstawowych własności działań jak przemienność, łączność i rozdzielność. Wzory skróconego mnożenia stosuje się w arytmetyce, algebrze i analizie; przykłady ich użycia to^[2]:

• przyspieszanie obliczeń, umożliwiające wykonanie pewnych działań arytmetycznych w pamięci;
• działania na pierwiastnikach, np.:
  • usuwanie niewymierności z mianowników – przekształcanie odwrotności takich wyrażeń, czyli ich minus pierwszej potęgi;
  • pierwiastkowanie ich – przekształcanie ich potęgi ułamkowej;
• przekształcenia równań kwadratowych i funkcji kwadratowych^[3][4];
• dowodzenie nierówności^[5];
• obliczanie granic ciągów^[6].

Wzory te są standardowym elementem wykształcenia matematycznego na poziomie średnim; przykładowo znalazły się one w podstawie programowej polskich liceów i techników, także w zakresie podstawowym^[7].

Wykładnik dwa – wzory z kwadratami

Kwadraty sum i różnic dwóch liczb

Dla dowolnych liczb rzeczywistych zachodzi^[8][1]:

${\displaystyle (a\pm b)^{2}=a^{2}\pm 2ab+b^{2}.}$

Przykłady zastosowań arytmetycznych – obliczanie^[2][9]:

• kwadratów liczb naturalnych:

${\displaystyle {\begin{aligned}102^{2}&=(100+2)^{2}=100^{2}+2\cdot 100\cdot 2+2^{2}=\\&=10\ 000+400+4=10\ 404;\end{aligned}}}$

${\displaystyle {\begin{aligned}297^{2}&=(300-3)^{2}=300^{2}-2\cdot 300\cdot 3+3^{2}=\\&=90\ 000-1\ 800+9=88\ 209;\end{aligned}}}$

• pierwiastków kwadratowych z pierwiastników:

${\displaystyle {\begin{aligned}{\sqrt {17+12{\sqrt {2}}}}&={\sqrt {3^{2}+({\sqrt {8}})^{2}+2\cdot 6{\sqrt {2}}}}=\\&={\sqrt {3^{2}+2\cdot 3\cdot 2{\sqrt {2}}+(2{\sqrt {2}})^{2}}}=\\&={\sqrt {(3+2{\sqrt {2}})^{2}}}=3+2{\sqrt {2}};\end{aligned}}}$

${\displaystyle {\begin{aligned}{\sqrt {14-6{\sqrt {5}}}}&={\sqrt {3^{2}+{\sqrt {5}}^{2}-2\cdot 3{\sqrt {5}}}}=\\&={\sqrt {(3-{\sqrt {5}})^{2}}}=3-{\sqrt {5}}.\end{aligned}}}$

Kwadraty sum więcej niż dwóch liczb

Wzory te mają również wersje dla większej liczby składników, np. dla trzech^[5]:

${\displaystyle (a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc.}$

Wzór ten można stosować dla kwadratu dowolnej liczby składników. Po prawej stronie wzoru wystąpią wtedy kwadraty każdego ze składników w nawiasie oraz podwojone iloczyny każdej pary tych składników^{[potrzebny przypis]}:

${\displaystyle \left(\sum \limits _{i=1}^{k}a_{i}\right)^{2}=\sum \limits _{i,j=1}^{k}a_{i}a_{j}.}$

Różnice można przedstawić w postaci sumy składników o przeciwnym znaku, np. ${\displaystyle (a-b-c+d)^{2}=(a+(-b)+(-c)+d)^{2}.}$

Wzory te mają także uogólnienie w przestrzeniach unitarnych, zwane tożsamością polaryzacyjną.

Różnice kwadratów

Różnica kwadratów dwóch liczb to iloczyn sumy tych liczb i ich różnicy^[1][8]:

${\displaystyle a^{2}-b^{2}=(a+b)(a-b).}$

Przykład zastosowania arytmetycznego – usuwanie niewymierności z mianownika^[2]:

${\displaystyle {\begin{aligned}{\frac {2}{{\sqrt {11}}-3}}&={\frac {2({\sqrt {11}}+3)}{({\sqrt {11}}-3)({\sqrt {11}}+3)}}=\\&={\frac {2({\sqrt {11}}+3)}{11-3^{2}}}={\frac {2(3+{\sqrt {11}})}{2}}=\\&=3+{\sqrt {11}}.\end{aligned}}}$

Sumy kwadratów

Analogiczna suma ${\displaystyle a^{2}+b^{2}}$ nie rozkłada się na wyrażenia rzeczywiste, jednak można rozłożyć ją na iloczyn liczb zespolonych^{[potrzebny przypis]}:

${\displaystyle a^{2}+b^{2}=(a+bi)(a-bi),}$ gdzie ${\displaystyle i}$ to jednostka urojona.

Wykładnik trzy – wzory z sześcianami

Sześcian sumy i różnicy^[8][1]:

${\displaystyle (a\pm b)^{3}=a^{3}\pm 3a^{2}b+3ab^{2}\pm b^{3}.}$

Suma i różnica sześcianów^[8][1]:

${\displaystyle a^{3}\pm b^{3}=(a\pm b)(a^{2}\mp ab+b^{2}).}$

Przykład zastosowania arytmetycznego – usuwanie niewymierności z mianownika^[10]:

${\displaystyle {\begin{aligned}{\frac {1}{{\sqrt[{3}]{9}}-2}}&={\frac {{\sqrt[{3}]{9}}^{2}+2{\sqrt[{3}]{9}}+2^{2}}{({\sqrt[{3}]{9}}-2)({\sqrt[{3}]{9}}^{2}+2{\sqrt[{3}]{9}}+2^{2})}}=\\&={\frac {{\sqrt[{3}]{3^{4}}}+2{\sqrt[{3}]{9}}+4}{9-2^{3}}}=\\&=4+3{\sqrt[{3}]{3}}+2{\sqrt[{3}]{9}}.\end{aligned}}}$

Wykładnik cztery

Różnica czwartych potęg

Różnicę czwartych potęg można obliczyć, korzystając z:

• tego, że czwarta potęga to kwadrat kwadratu;
• podanego wyżej wzoru na różnicę kwadratów.

Wynik^[11]:

${\displaystyle {\begin{aligned}a^{4}-b^{4}&=(a^{2})^{2}-(b^{2})^{2}=\\&=(a^{2}-b^{2})(a^{2}+b^{2})=\\&=(a-b)(a+b)(a^{2}+b^{2}).\end{aligned}}}$

Ostatni wzór można też zapisać inaczej, mnożąc sumę kwadratów ${\displaystyle (a^{2}+b^{2})}$ przez sumę ${\displaystyle (a+b)}$ lub różnicę ${\displaystyle (a-b)}$^[12]:

${\displaystyle {\begin{aligned}a^{4}-b^{4}&=(a-b)(a^{3}+a^{2}b+ab^{2}+b^{3})=\\&=(a+b)(a^{3}-a^{2}b+ab^{2}-b^{3}).\end{aligned}}}$

Pierwszy z tych wzorów jest analogiczny do podanego wyżej wzoru na różnicę sześcianów. Ma też uogólnienie na dowolny wykładnik naturalny, podane niżej.

Tożsamość Sophie Germain

Suma czwartej potęgi oraz czterokrotności czwartej potęgi zawsze jest iloczynem dwóch wyrażeń kwadratowych (stopnia drugiego)^[13]:

${\displaystyle {\begin{aligned}a^{4}+4b^{4}&=(a^{2}+2ab+2b^{2})(a^{2}-2ab+2b^{2})=\\&={\Bigl (}(a+b)^{2}+b^{2}{\Bigr )}{\Bigl (}(a-b)^{2}+b^{2}{\Bigr )}.\end{aligned}}}$

Ta tożsamość algebraiczna znajduje zastosowania w arytmetyce – zarówno elementarnej, jak i wyższej – oraz algebrze i analizie. Z pomocą tej równości można:

• obliczać niektóre sumy i iloczyny, skończone^[13] lub nie^[14];
• dowodzić, że niektóre liczby całkowite zapisane wprost lub wzorami są złożone^[13][14][15];
• badać rozkładalność niektórych dwumianów o współczynnikach całkowitych^[14];
• rozwiązywać niektóre równania diofantyczne^[14].

Wzory ogólne

Potęgi sum i różnic

Potęga naturalna sumy dwóch składników to szczególny przypadek dwumianu Newtona^[12]:

${\displaystyle (a+b)^{n}=\sum _{k=0}^{n}{n \choose k}a^{n-k}b^{k}.}$

${\displaystyle (a-b)^{n}=\sum _{k=0}^{n}(-1)^{k}{n \choose k}a^{n-k}b^{k}}$

Potęga naturalna sumy dowolnej skończonej liczby składników to^{[potrzebny przypis]}:

${\displaystyle \left(\sum \limits _{i=1}^{k}a_{i}\right)^{n}=\sum \limits _{m_{1},\dots ,m_{k}=0}^{n}{n \choose m_{1},\dots ,m_{k}}\prod \limits _{i=1}^{k}a_{i}^{m_{i}},}$

gdzie ${\displaystyle {n \choose m_{1},\dots ,m_{k}}={\frac {n!}{\prod \limits _{i=1}^{k}m_{i}!}}.}$

Różnice i sumy potęg

Różnica dwóch potęg tego samego stopnia naturalnego to^[12]:

${\displaystyle a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^{2}+\ldots +ab^{n-2}+b^{n-1})}$

Przykład – różnica piątych potęg^[11]:

${\displaystyle a^{5}-b^{5}=(a-b)(a^{4}+a^{3}b+a^{2}b^{2}+ab^{3}+b^{4}).}$

Oprócz tego^[12]:

${\displaystyle a^{2n+1}+b^{2n+1}=(a+b)(a^{2n}-a^{2n-1}b+a^{2n-2}b^{2}-\ldots -ab^{2n-1}+b^{2n})}$

Przykład – suma piątych potęg^[11]:

${\displaystyle a^{5}+b^{5}=(a+b)(a^{4}-a^{3}b+a^{2}b^{2}-ab^{3}+b^{4}).}$

Przypisy

Bibliografia

• Wojciech Babiański, Lech Chańko, Joanna Czarnowska, Grzegorz Janocha, Dorota Ponczek, Jolanta Wesołowska: Matematyka 2. Podręcznik dla liceum ogólnokształcącego i technikum. Wydawnictwo Nowa Era, 2020. ISBN 978-83-267-3900-2.
• Tomasz Kobos. Tożsamość Sophie Germain. „Kwadrat. Gazetka Olimpiady Matematycznej Gimnazjalistów”, s. 3, lipiec 2015. Stowarzyszenie Edukacji Matematycznej. ISSN 2300-0708. [dostęp 2024-05-07]. 
• Włodzimierz Krysicki, Lech Włodarski: Analiza matematyczna w zadaniach. Wyd. XXI. T. 1. Warszawa: Wydawnictwo Naukowe PWN, 1994. ISBN 83-01-01460-1.